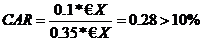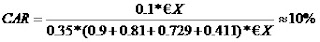Conventional economic theory states that banks are bounded by their reserve requirements when it comes to creating new money. In the conventional way, if just one bank exists in the economy, the money multiplier roughly equals the inverse of the reserve ratio. For example, if banks are required to hold a 10% reserve ratio, then the value of the multiplier is roughly 10. Thus if money introduced in the economy via the government is M then with the banks' assistance they will reach 10M. (for a more detailed analysis and some examples, Wikipedia provides an excellent introduction)
Nevertheless, the idea that the money multiplier is a myth, in its conventional estimation at least, has been promoted by a number of academics and non-academics. Notably, a 2010 paper by the Washington Federal Reserve questions its existence while a recent article by Scott Fullwiler does an excellent work in explaining the endogenous money theory (which basically states that banks are not constrained by deposits but by regulatory capital requirements) as well as the interactions between the economy and monetary and fiscal policies. What has been left unanswered, however, has been whether a money multiplier exists in the endogenous money theory and whether this may be calculated up to any degree. It is this author's belief that both of the above questions can be solved and the answer is affirmative in both case.
Model:
Consider an economy with just one bank. The bank chooses to invest the money it receives in one of the following types of assets, depending on its risk appetite and the risk-return relationship. Each asset has its own specific risk weight which is as defined by the Basel II capital adequacy rules (in the case where the asset types could have more than just 1 risk-weight value, I have assumed for simplicity the lowest)
1. Government bonds (0%)
2. Loans to corporates or securities companies (20%)
3. Retail Loans (75%)
4. Secured residential property loans (35%)
5. Secured commercial real estate loans (100%)
6. Other loans (100%)
7. Cash (0%)
Now suppose that at time 0 we witness an influx of €X of new money in the economy (again for simplicity we assume that no cash in circulation exist. The reader may find it easier to understand this as an economy where every transaction is carried out via a credit/debit card and subsequently when an account is debited another is credited). The money, (which as we have seen here is basically a transfer from the government to the people) is subsequently deposited in a bank. Then, it is up to the bank's discretion to select one of the 7 asset choices mentioned above. Through the analysis, the assumption is that the bank holds €0.1X in equity and the minimum capital requirement is 10%.
If, for example, the bank chooses to invest in option 7, then the currency available in the economy does not change at all. Using the broad definition of M2 (can be found here) if the money deposited in the bank stays in the bank as cash, then the money stock is exactly equal to €X. In this case, it is more than obvious that the money multiplier value is exactly 0.
Now suppose that the bank decides to invest fully in loans secured by residential property. Then, the first time these funds are lent out the bank has a risk weight of 0.35*€X. Thus, the bank's capital ratio will be:
Thus, the bank after producing the aforementioned loans, still has a margin of 18% which is to its best interest to use; which means that the bank will choose to lend again and again until the ratio equals 10%.
The value of the multiplier here is essentially based on the amount of money lent out. Thus, since the money supply in the economy has been increased by 285%, the money multiplier is 2.85, or exactly 1/0.35. In other words, if the initial money supply was €1bn, then the bank was able to raise the amount of money in the economy to €3.85bn with just €100m of equity.
Money Multiplier Using Reserves
While in the previous example we have not used the notion of bank reserves at all, we will now show that these do not matter at all to the money multiplier (i.e. they do not affect the multiplier value). Suppose now that the bank has to save 10% of its existing deposits each time, or in other words it can only lend 90% of its existing deposits. Now, the capital requirement ratio for the first round of lending will become
Continuing with our substitutions, we find that the multiplier value which will again make the regulatory capital equal 10% will be 2.85, yet it will be reach in an additional round of lending
Thus, any change in the reserves ratio does not have any affect whatsoever on the multiplier value. All it does is make the rounds of lending until the final value is reached more. In addition, what can also be inferred from the above analysis is that a Y% increase in equity will mean a similar Y% increase in the multiplier value. The following graph indicates the multiplier values for 0.1X equity (solid line) and the effect a 20% increase on the equity value (dashed line).
What is considered as a fact (regardless of the approach) is that approximately 90% of the money supply in the economy comes as a result of the banking sector. Nevertheless, as we have seen above, the multiplier appears to be very small to accommodate such an increase in the money supply. In fact, the banks in this model represent about 75% of the money supply under the 35% risk weight assumption; if the weight is at the low of 20% then the banks represent up to 83% of the supply of money. What the reader should note is that these values are much larger than real-life ones, as it is customary that a bank would choose a combination of the above assets and not just focus on a specific asset category.
An issue which would further increase the amount of money in the economy would be the introduction of a new bank. If a new bank enters the market then the maximum value of the multiplier given the asset selection has been reached, then money supply may be increased, again up to the point where capital regulations allow it. If, for example, bank 2 has an equity value of 0.05X then the money supply in the economy can be increased by 1.425, making bank-created money supply reach 82% of the total money in the economy. Thus, after many more banks are considered in the economy, with each bank contributing to the total money supply (yet, not all banks having the same equity values) the bank-created money would reach approximately 90% (or even higher) of the total money stock. The same would occur if 2 (or more) banks were in the economy at time 0.
The above model presents what the author understands to be a much better representation of the money multiplier values. As we have seen, these values are heavily determined by the bank's equity and (most importantly) the investment decisions each bank chooses to make. Although we cannot pinpoint the exact value of the money multiplier, we can be sure that this has no relation to the reserve ratio. In addition, the number of banks in the economy plays an important role to the total money stock, although their individual multiplier values are constrained just by their equity.
The policy implications of the money multiplier will be duly discussed in a follow-up post.
An issue which would further increase the amount of money in the economy would be the introduction of a new bank. If a new bank enters the market then the maximum value of the multiplier given the asset selection has been reached, then money supply may be increased, again up to the point where capital regulations allow it. If, for example, bank 2 has an equity value of 0.05X then the money supply in the economy can be increased by 1.425, making bank-created money supply reach 82% of the total money in the economy. Thus, after many more banks are considered in the economy, with each bank contributing to the total money supply (yet, not all banks having the same equity values) the bank-created money would reach approximately 90% (or even higher) of the total money stock. The same would occur if 2 (or more) banks were in the economy at time 0.
The above model presents what the author understands to be a much better representation of the money multiplier values. As we have seen, these values are heavily determined by the bank's equity and (most importantly) the investment decisions each bank chooses to make. Although we cannot pinpoint the exact value of the money multiplier, we can be sure that this has no relation to the reserve ratio. In addition, the number of banks in the economy plays an important role to the total money stock, although their individual multiplier values are constrained just by their equity.
The policy implications of the money multiplier will be duly discussed in a follow-up post.